——前言——

Cox回归由于其复杂性和相对较少应用（除了临床研究），很多统计学习者很少接触，对其原理与应用不甚了解，一般医学教科书一写到Cox回归，马上会涉及到几个令人生畏的名称：比如半参数回归、风险函数，以及那无法理解的Cox回归方程。当然Cox回归全称也令人发蒙：“Cox比例风险模型”。

但随着队列研究和中长期随访的实验性研究越来越多，了解Cox回归是一项必要的学习内容。本文撇开复杂原理，简单通俗地介绍下Cox回归，特别是它的应用。除此之外，必须值得了解的一个非常重要的指标--HR值。

——COX回归与HR值——

科学研究中，经常遇到分类的结局，主要是二分类结局（阴性/阳性；生存/死亡），研究者可以通过logistic回归来探讨影响结局的因素，或者构建预测模型来预测患者的预期结局。

但很多时候logistic回归方法无法使用。比如，在随访期中，绝大部分对象都发生阳性结局( 患者全部治愈或者患者几乎都死亡了)。例如比较两种治疗手段治疗新冠肺炎效果（比如瑞德西韦和安慰剂组），可能在1一个月的效果分别是95%和90%，在统计学上可能没有差异。

logistic回归是关于率的分析，探讨影响发生率的因素，但发生率的研究不能说明一切。

不过，我们还可以从发生率发生的速度来分析，探讨影响发生速度的因素。这便是Cox回归基本思维。

Cox回归是生存分析的重要方法，全称是“Cox比例风险模型”。它主要探讨终点事件发生速度有关的因素。通俗来说，它可以探讨，到底哪类群体的“死亡”速度更快、到底什么因素影响了“死亡”速度。

生存分析的“死亡”指的是，阳性终点事件的发生。死亡速度指的是，t时刻存活的个体在t 时刻的瞬时死亡（阳性事件发生）率，可以理解为一组人群在不同时刻的阳性终点事件发生的速度。具体可以用以下函数来表达：

\(h(t) = \frac{P (t\leq T < t + \Delta t | T \geq t)} {\Delta t}\)

在专业上，我们把它称之为风险h(t)，上述公式称之为风险函数（hazard function）。风险值随着时间的变化而变化，一般情况下，随访前期，“死亡“速度较快。

因此，Cox回归是关于“死亡”风险的研究。但是上述公式无法将死亡风险与相关因素建立起联系。

终于在1972年，由英国统计学家D.R.CoxCox建立了新的函数，来解决这个问题。

\(h(t) = h_{0}(t) e ^ {(\beta_{1}x_{1}+\beta_{2}x_{2}+...+\beta_{j}x_{j})}\)

或者写成：

\(h(t) = h_{0}(t) exp (\beta_{1}x_{1}+\beta_{2}x_{2}+...+\beta_{j}x_{j})\)

h(t) 便是研究对象的风险函数，即“死亡”速度，它随着时间的变化而变化。h0（t）是回归方程的截距，初学者完全可以忽略；x1，x2，…xj是自变量，β1，β2…，βj为回归系数。

可以发现，Cox回归是一种嵌套线性方程的模型。它通过指数转换，建立了新的线性回归方程，用于探讨自变量x对因变量h（t）的影响，一种非线性的影响。

我先举个简单的单因素Cox回归分析案例：

比较男性和女性白血病患者缓解时间（天）的差异性，各自的生存时间如下：

男性：4，5，9，10，11，12，13， 20+，28，28，28，29，31，32，37，41，41，57，62，74，109，100，139，158+

女性：8，10，10，12，14，20，48，70，75，99，103，161+，162，169，195，199+，220，217+，245+

本案例中疗法的终点阳性事件是疾病进展，男性和女性有不同的生存时间，研究目的是分析性别与生存情况的关系。

我们可以从死亡速度的角度进行分析。根据生存曲线（下图），可以得知不同组的“死亡”速度，即疾病进展速度是不同的，从而造成生存率变化趋势不同。

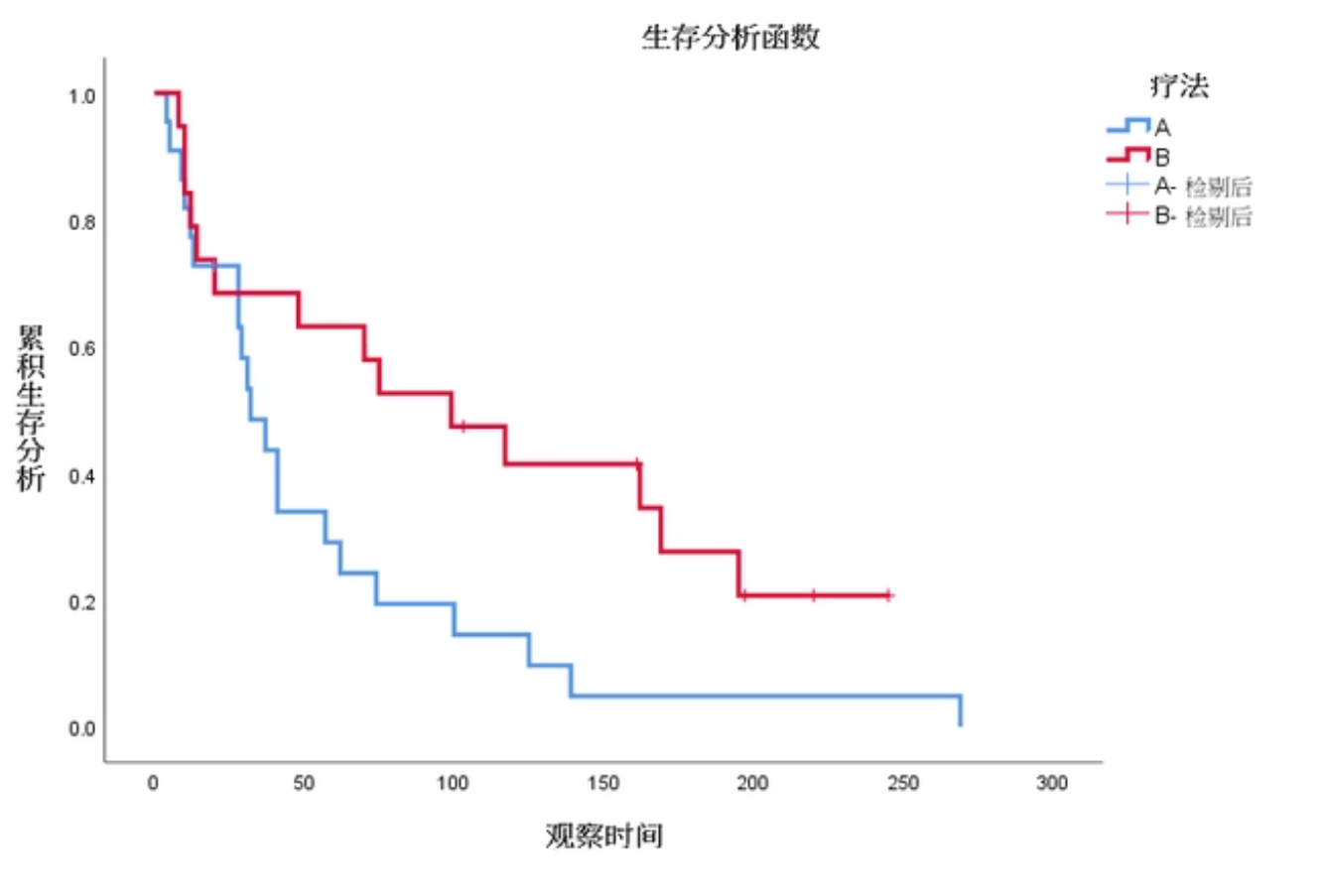
如果形成Cox回归，那就是：

\(h(t) = h_{0}(t) exp (\beta_{性别} * X_{性别} )\)

这是风险函数h(t)与性别x的关系。通过这个公式，可以分别求男性的死亡速度h(t)和女性的死亡速度h(t)。

对于性别与疾病进展速度的关系，我们最想知道，女性相对于男性，“死亡”速度升高了还是降低了？升高了多少倍？降低了多少比例？即：

\(\frac{h_{女}(t)}{h_{男}(t)} = ?\)

女性和男性相比，对结局的直接影响便是β，它含义是，X从男性变化到女性对结局的影响程度。

但这种影响并非是“死亡”速度的影响，因为死亡数和性别没有直接的线性关系。实际上，我可以分别带入男性和女性数据库赋值（男性=1，女性=2）来看看两者的关系。

\(\begin{align} \frac{h_{女}(t)}{h_{男}(t)} &= \frac{h_{0}(t)e^{(\beta_{1} * 2)}}{h_{0}(t)e^{(\beta_{1} * 1)}} \\ & = e ^ {(\beta_{1} * 2 - \beta_{1} * 1)} \\ & = e ^ {[\beta_{1} * (2 - 1)]} \\ & = e^{\beta} \end{align}\)

从这一结果可以看出，女性的死亡速度h(t)和男性的死亡速度h(t)比值，它不等于β，而是等于自然指数e的β次方，e^β即EXP（β）。我们可以构建Cox回归方程，计算出β=-0.784，则EXP（β）=0.456，也就是女性相对男性，死亡速度总体将降低54.4%。

因此通过构建风险函数有关的Cox模型，可以探讨和比较不同组别对风险函数值的影响，利用β和XP（β）分析研究因素的相对影响。β值绝对值越大，EXP（β）越远离1，说明相对作用越大。

其中，EXP（β）直接反应了死亡速度的相对大小。当EXP（β）=1，说明两组人群“死亡”速度相当；当EXP（β）>1，且值越大，说明女性的风险越大，当EXP（β）<1，且值越小，说女性的“死亡”风险越小。当EXP（β）=2，说明女性死亡速度是男性的2倍；当EXP（β）=0.5，说明女性死亡速度是男性的一半。

EXP（β），我们称之为风险函数值比值，简称风险比，HR；它是两个率之比，属于相对危险度RR值的一种（关于相对危险度，可以了解前文：队列研究的基本统计分析策略）。

\(HR_{j} = exp (b_{j}) = e^{b_{j}}\)

• HR值大于1，提示暴露是阳性事件发生的促进因素；
• HR值小于1，提示暴露是阳性事件发生的阻碍因素；
• HR值等于1，提示暴露对阳性事件的发生无影响。

HR值虽然意思与之前介绍过的RR值略有不同（队列研究的基本统计分析策略），但意义相同。两者统称为相对危险度。它们均反映自变量对阳性结局的影响程度，表示的是暴露相对于对照（干预相对于对照）对阳性事件发生造成的影响。它们都能直观地表达为影响的倍数或者比例。比如HR或者RR =2，说明暴露组相对对照组，阳性事件发生风险增加1倍。

HR、RR与OR值在解释上存在着不同，OR值不能直接表达阳性事件发生风险的倍数与比例，它值接近于RR值，但不等于RR。

——生存分析的目的与COX回归的作用——

具体来说，根据研究目的，生存分析的研究内容可以分为以下4点：

1. 描述生存过程，计算生存时间、计算生存率（或者死亡率）、计算死亡速度

2. 比较生存过程，比较生存时间、比较生存率（或者死亡率）、比较死亡速度

3. 探讨影响生存时间（生存速度）的影响因素

4. 预测生存概率

不同的生存分析内容，有不同的统计分析策略：

1. 描述生存过程方面，一般采用经典的寿命表法或者 或者Kaplan-Meier法来计算生存率、计算中位生存时间、并且用生存曲线的方式来描述生存过程

2.比较生存过程方面，一般采用logRank或者广义秩和检验的方法开展生产时间资料分布的组间差异性

3.探讨影响生存时间（生存速度）的影响因素、预测生存概率方面，最常用也是最经典的便是Cox回归分析。

因此，Cox回归在观察性研究中和其它回归方法一样是压舱石，是最重要的分析武器。

Cox回归与logistic回归一样，同样可以开展单因素Cox回归和多因素Cox回归，单因素Cox回归是简单关联性分析比较，而多因素Cox回归可以探讨多种因素对生存结局的影响。因此，一般Cox回归都需要开展多因素回归分析的方法。